Números Complejos Resumen

Números complejos 1.

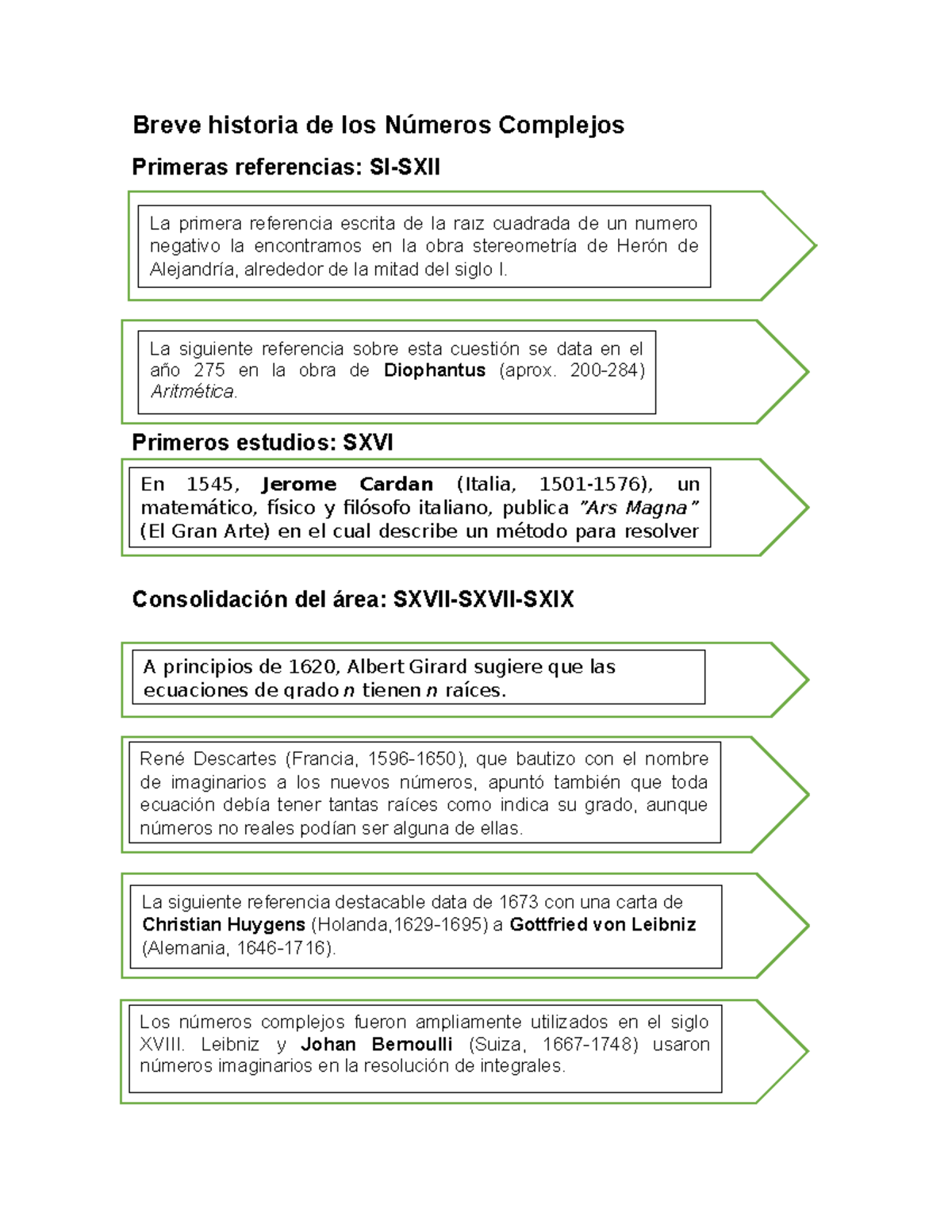
Números complejos resumen. Números Complejos Ingeniería de Telecomunicación Fundamentos Matemáticos I 2 Necesidad de ampliar el conjunto de los números reales Definición El conjunto de los números complejos se define como el. Z a bi donde a y b son números reales e i la unidad imaginaria. Números Complejos r ea b φ 2k π k Z Esto significa que un número complejo tiene infinitos logaritmos neperianos.

Antes hemos definido la suma de dos números complejos puestos como pares de la forma. Una lista de los puntos de resumen de la lección que han estudiado los Números complejos de módulo Module 1. Surge de la necesidad de que el alumno de ingeniería puedautilizarlo como una herramienta de apoyo para estudio el de la materia de Álgebra en I denominado I NÚMEROS COMPLEJOS del programa actual así como de materias afines.

Números Complejos Mate máticas 1 1 Elena Álvarez Sáiz Dpto. Para multiplicar números complejos que son binomios usar la Propiedad Distributiva de la Multiplicación o el método FOIL. Multiplicar los términos resultantes.

Este término fue destacado por René Descartes en el siglo XVII y expresaba claramente sus creencias. Módulo y argumento de números complejos. Z 3 2 i.

Nos referimos a lo siguiente. Los números complejos se utilizan en todos los campos de las matemáticas en muchos de la física y en ingeniería especialmente en la electrónica y las telecomunicaciones por su utilidad para representar las ondas electromagnéticas y la corriente eléctrica. Umple con el objetivo de dicho.

Hoy en día ubicamos los números imaginarios sobre el eje vertical del plano complejo. Números complejos en forma polar y trigonométrica. Cuáles son los números complejos y los números reales Empezamos conociendo con detalle la definición de los números reales y complejos para que así puedas entender mejor la teoría.